De stelling van Pythagoras hoe het werkt, voorbeeldsommen & zelf oefenen YouTube
Stelling van Pythagoras Poster in de Klas

Dus, met de stelling van Pythagoras kunnen we, als we 2 zijden van de rechthoekige driehoek weten altijd de derde berekenen. En voordat ik je toon hoe je dat moet doen, zal ik je eerst nog wat terminologie (woordenschat) aanleren. De langste zijde van een rechthoekige driehoek is de overstaande zijde van de rechte hoek (90 graden).
Stelling van Pythagoras hoe werkt het? Mr. Chadd Academy

De stelling van Pythagoras. In een rechthoekige driehoek wordt het verband tussen de lengten a en b van de twee rechthoekszijden en de lengte c van de schuine zijde gegeven door: a 2 + b2 = c2. De zijde c noemen we ook wel de hypotenusa. De stelling van Pythagoras is een belangrijke stelling. Bij tal van berekeningen en bewijzen van andere.
Stelling van Pythagoras hoe werkt het? Mr. Chadd Academy
De stelling van Pythagoras stelt dat de som van de kwadraten van de kortere zijdes, dus a kwadraat plus 9 kwadraat gelijk zal zijn aan 14 in het kwadraat.. Als je een gevoel wilt krijgen hoe groot ongeveer de wortel van 115 is, bedenk dan, de wortel van 100 is gelijk aan 10. En de wortel van 121 is gelijk aan 11. Dus de waarde hier zal.
stelling van pythagoras rechthoekzijde berekenen Wiskunde TV YouTube
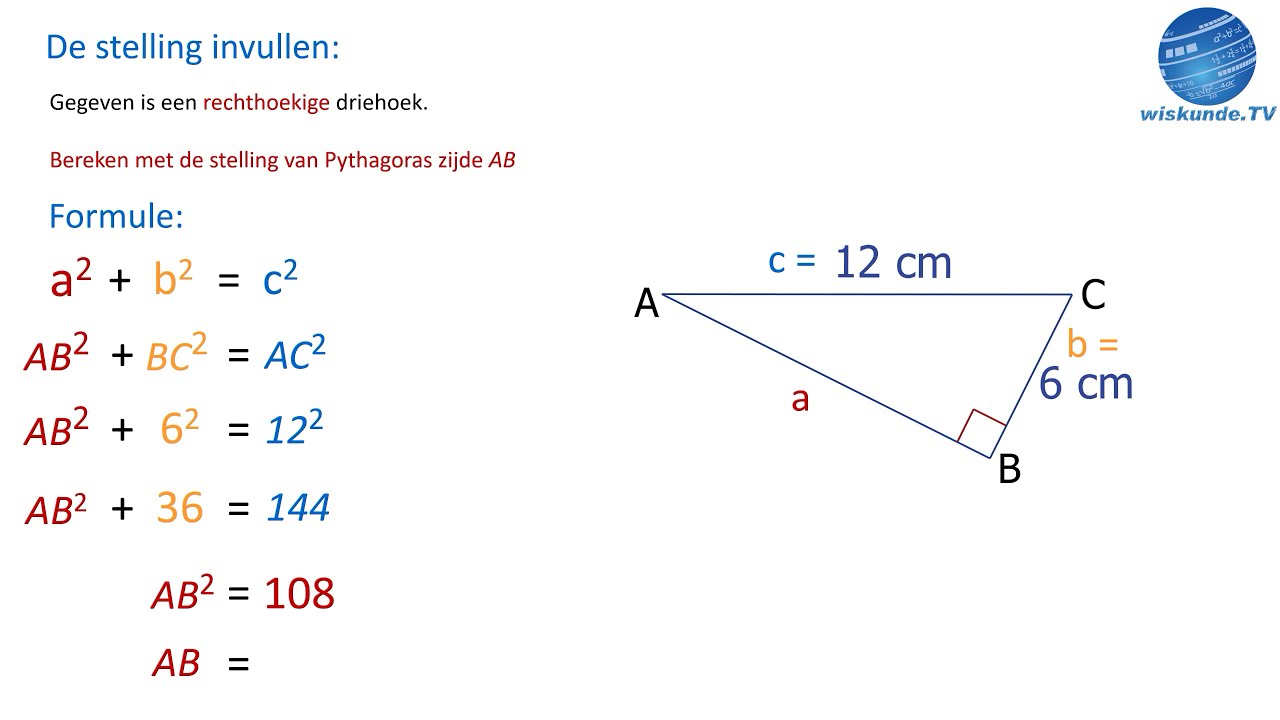
De stelling van Pythagoras. Een rechthoekige driehoek heeft 3 zijdes: 2 rechthoekszijden en een schuine zijde. De schuine zijde wordt ook wel eens de langste zijde, of de hypotenusa genoemd. Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a 2 + b 2 = c 2.
Hoe Bereken Je De Stelling Van Pythagoras Een Eenvoudige Uitleg Liugems

De stelling van Pythagoras (SvP) is natuurlijk een heel mooie stelling die handige toepassingen heeft. Denk daarbij bijvoorbeeld aan het omgekeerde van de stelling: als je een 3:4:5 driehoek maakt (verhouding van de zijden, bijvoorbeeld met drie stukken hout) dan heb je met zekerheid een rechte hoek geconstrueerd tussen die 3:4 zijden.
Stelling van Pythagoras voorbeeld 1 YouTube

De stelling geldt voor alle rechthoekige driehoeken, ongeacht of de lengten van de zijden een heel, een rationeel of irrationeel getal is. De stelling van Pythagoras stelt dat bij een rechtloekige driehoek de som van de kwadraten van de twee korte zijden gelijk is aan het kwadraat van de lange zijde. Als formule: a 2 + b 2 = c 2.
Stelling van Pythagoras en bekende driehoeken YouTube

Toets je begrip over Stelling van Pythagoras met deze NaN vragen. De stelling van Pythagoras beschrijft een speciaal verband tussen de zijden van een rechthoekige driehoek. Heel vroeger was de mensheid al bekend met dit verband. In dit onderwerp gaan we uitzoeken hoe je de stelling van Pythagoras kan gebruiken en bewijzen we waarom het werkt.
Hoedoeje Hoe werkt de stelling van pythagoras YouTube

Eindtoets beginnen. De stelling van Pythagoras beschrijft een speciaal verband tussen de zijden van een rechthoekige driehoek. Heel vroeger was de mensheid al bekend met dit verband. In dit onderwerp gaan we uitzoeken hoe je de stelling van Pythagoras kan gebruiken en bewijzen we waarom het werkt.
PPT De stelling van Pythagoras PowerPoint Presentation, free download ID3915661

Uiteraard willen we weten hoe lang de schuine zijde is. Met de stelling van Pythagoras is dat geen probleem: a²+b²=c². We stellen de zijde 2 gelijk aan a en de zijde met lengte 5 gelijk aan b. We vullen dit in onze formule in en krijgen zo 2²+5²=c². We rekenen dit uit: 2²+5² = 4+25 = 29. Dus 29=c², of c²=29.
Wiskunde Hoe gebruik ik de stelling van Pythagoras? YouTube

De stelling van Pythagoras is als volgt: a² + b² = c². Hierbij geldt dat a en b de rechthoekszijden zijn (dus de zijden aan de rechte hoek) en c de schuine zijde. Dit is terug te zien in het plaatje. Als je de lengtes van 2 zijden van de driehoek weet, dan kan met behulp van de stelling van Pythagoras de derde zijde worden berekend.
Bewijs stelling van Pythagoras + enkele voorbeelden YouTube

Eén zijde is onbekend, je weet niet hoe lang deze is. Wel, met behulp van Pythagoras rekenen we dit uit. De stelling van Pythagoras geeft ons de relatie weer van alle drie de zijden. Stel, we hebben een driehoek met rechthoekszijden 2 en 5. We willen weten hoe lang de schuine zijde is. Geen probleem! Onze held Pythagoras helpt ons: a²+b²=c².
De stelling van Pythagoras WRTS
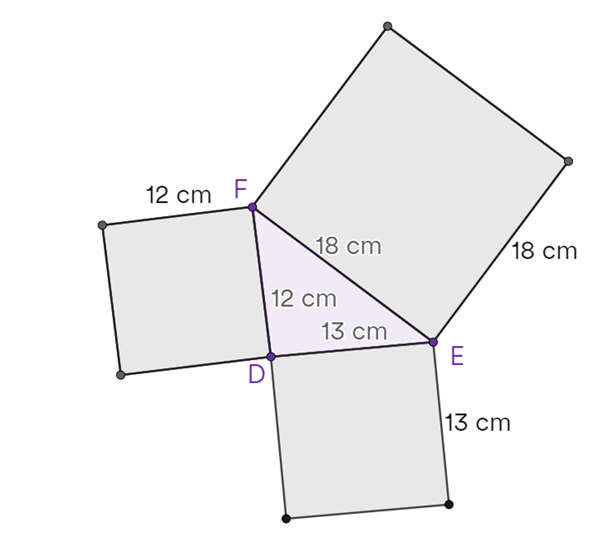
Stelling. De stelling van Pythagoras geeft een verband tussen de lengten van de zijden van een rechthoekige driehoek. Noemt men de lengten van rechthoekszijden, de zijden die aan de hoek van 90° liggen, en , en de lengte van de schuine zijde, de zijde die niet aan de rechte hoek grenst, de hypotenusa, , dan is de bekende wiskundige vorm van de.
Hoe Werkt De Stelling Van Pythagoras In De Praktijk?

Gebruik deze video's als ondersteuning van je huiswerk of in de klas. Neem de boel niet domweg over, maar bekijk eerst de video en maak dan zelf je huiswerk. 1 Zeer goede video's voor Wiskunde A en B. Tevens laten we je ervaren hoe goed Geogebra is! 2 De video's zijn opgaven uit je schoolboek en geven meer inzicht!
Stelling van Pythagoras in Geogebra YouTube

Wat is de stelling van Pythagoras en wat kan je ermee? In deze video bekijken we een voorbeeld waar je ziet hoe je vraagstukken oplost met Pythagoras.Vragen.
Wiskunde stelling van Pythagoras.wmv YouTube

Onthoudt daarom de stelling van Pythagoras in de algemene vorm: (ene rechthoekszijde)2 + (andere rechthoekszijde)2 = (schuine zijde)2. Of ook wel bekend als: a2 + b2 = c2, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is. Met Slimleren kun je op een leuke manier thuis extra oefenen met de vakken waar jij moeite mee hebt.
Top 53 Hoe Werkt De Stelling Van Pythagoras Update

Stelling van Pythagoras: hoe werkt het? - Mr. Chadd AcademyEen rechthoekige driehoek is een driehoek met een hoek van 90 graden.Als een driehoek geen rechte.